Embark on a captivating journey through Eureka Math Algebra 1 Module 3, where the enigmatic world of algebra unfolds before your eyes. This module is a treasure trove of knowledge, meticulously crafted to equip you with the foundational skills and concepts that will illuminate your path towards algebraic mastery.

Prepare to unravel the intricacies of linear equations and inequalities, delve into the fascinating realm of functions, and conquer the challenges posed by systems of equations and inequalities. Eureka Math Algebra 1 Module 3 is your passport to unlocking the secrets of algebra, empowering you to solve complex problems and unravel the mysteries of the mathematical universe.

Module Overview

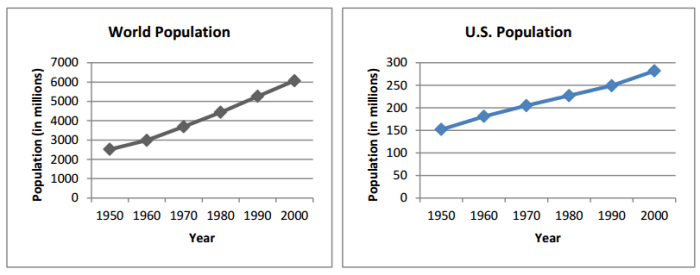
Eureka Math Algebra 1 Module 3 delves into the realm of linear equations and inequalities, laying a solid foundation for students to explore the intricate world of algebra.

This module empowers students with the tools to solve linear equations and inequalities, equipping them with essential skills for future mathematical endeavors. It emphasizes the significance of representing solutions graphically and algebraically, nurturing their understanding of linear relationships.

Solving Linear Equations

In this section, students embark on a journey to solve linear equations, mastering techniques to isolate the variable and find its value. They explore the concept of equivalent equations, recognizing that equations can be transformed without altering their solutions.

Solving Linear Inequalities

Expanding their mathematical horizons, students delve into the world of linear inequalities, learning to represent solutions graphically and algebraically. They discover the concept of compound inequalities and explore the properties of inequalities, developing a comprehensive understanding of their behavior.

Systems of Linear Equations

The module culminates with the exploration of systems of linear equations, where students learn to solve systems by graphing, substitution, and elimination. They investigate the concept of solution sets and explore special cases, such as inconsistent and dependent systems.

Unit 1: Linear Equations and Inequalities

Unit 1 of Eureka Math Algebra 1 introduces the fundamental concepts of linear equations and inequalities. These mathematical tools are essential for understanding and solving real-world problems involving linear relationships.

Linear Equations

A linear equation is an algebraic equation of the first degree, meaning it contains variables raised to the power of one and constants. Linear equations can be written in the form ax + b = c, where a, b, and care constants and xis the variable.

Methods to Solve Linear Equations

• Substitution Method:Substituting a known value for the variable in the equation to solve for the other variable.
• Elimination Method:Adding or subtracting equations to eliminate one variable and solve for the other.
• Graphical Method:Graphing the equation and finding the point where it crosses the x-axis or y-axis.

Linear Inequalities

A linear inequality is an algebraic inequality of the first degree, which means it contains variables raised to the power of one and constants. Linear inequalities can be written in the form ax + b < c, ax + b > c, ax + b ≤ c, or ax + b ≥ c, where a, b, and care constants and xis the variable.

Methods to Solve Linear Inequalities

• Graphing Method:Graphing the inequality and shading the region that satisfies the inequality.
• Algebraic Method:Solving the inequality algebraically by isolating the variable on one side of the inequality sign.

Examples, Eureka math algebra 1 module 3

Examples of solving linear equations and inequalities:

• Solve the equation: 2x + 5 = 13
• Solve the inequality: 3x- 4 < 10
• Graph the inequality: y > 2x + 1

Unit 2: Functions

Functions are mathematical relationships that assign to each element of a set a unique element of another set. Functions are essential in mathematics and have many applications in science, engineering, and other fields.Key characteristics of functions include:

• -*Domain

  The set of all possible input values.

-*Range

The set of all possible output values.

-*One-to-one

A function is one-to-one if each input value corresponds to only one output value.

-*Onto

A function is onto if each output value corresponds to at least one input value.

Types of Functions

There are many different types of functions, including:

• -*Linear functions

  Functions whose graphs are straight lines.

-*Quadratic functions

Functions whose graphs are parabolas.

The Eureka Math Algebra 1 Module 3 offers a comprehensive approach to mastering algebraic concepts. It’s like building blocks, each lesson adding a new piece to the mathematical puzzle. And speaking of puzzles, have you ever wondered if Rosie Revere, the inspiring character from the children’s book series, is based on a real person? Check out this article to unravel the mystery.

Back to our algebra journey, Eureka Math Module 3 empowers students with the tools to solve equations, simplify expressions, and navigate the world of polynomials.

-*Exponential functions

Functions whose graphs are exponential curves.

Graphing Functions

There are several methods for graphing functions, including:

• -*Plotting points

  This involves finding the coordinates of several points on the graph and then connecting them with a smooth curve.

-*Using a table of values

This involves creating a table of input and output values and then plotting the points on a graph.

-*Using a graphing calculator

This involves entering the equation of the function into a graphing calculator and then using the calculator to generate a graph.

Unit 3: Systems of Equations and Inequalities

In this unit, we will explore the world of systems of equations and inequalities. These mathematical constructs are used to represent and solve real-world problems involving multiple variables.

Types of Systems of Equations and Inequalities

Systems of equations and inequalities come in various forms, each with its unique characteristics:

• Systems of Linear Equations:These systems involve equations with variables raised to the first power (linear). They can be classified as consistent (having one or more solutions), inconsistent (having no solutions), or dependent (having infinitely many solutions).
• Systems of Nonlinear Equations:These systems involve equations with variables raised to powers other than one (nonlinear). They can be more challenging to solve and may have multiple solutions.
• Systems of Linear Inequalities:These systems involve inequalities with variables raised to the first power (linear). They represent regions in the coordinate plane that satisfy the given conditions.
• Systems of Nonlinear Inequalities:These systems involve inequalities with variables raised to powers other than one (nonlinear). They represent more complex regions in the coordinate plane.

Methods for Solving Systems of Equations and Inequalities

There are several methods for solving systems of equations and inequalities, including:

• Substitution:Solving one equation for a variable and substituting it into the other equation.
• Elimination:Adding or subtracting equations to eliminate one variable.
• Matrix Methods:Using matrices to represent and solve systems of equations.
• Graphing:Graphing the equations or inequalities and finding the points of intersection or overlap.

Examples of Solving Systems of Equations and Inequalities

Let’s consider some examples to illustrate the process of solving systems of equations and inequalities:

1. Solving a System of Linear Equations:Solve the system 2x + 3y = 11 and x
   

   y = 1.

2. Solving a System of Nonlinear Equations:Solve the system y = x^2 and x + y = 5.
3. Solving a System of Linear Inequalities:Graph the system of inequalities y > x + 1 and y< 2x - 1 to find the feasible region.
4. Solving a System of Nonlinear Inequalities:Graph the system of inequalities y > x^2 and y< 2x + 1 to find the feasible region.

Unit 4: Exponents and Polynomials

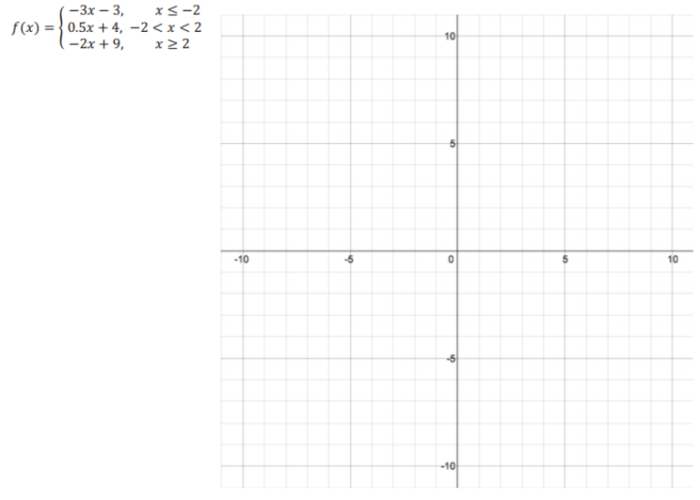
In this unit, we’ll explore the fascinating world of exponents and polynomials. We’ll start by understanding the concept of exponents and their properties, then delve into the different types of polynomials and their operations. Finally, we’ll equip ourselves with methods to factor polynomials, unlocking their hidden structures.

Exponents and Their Properties

• Exponents represent repeated multiplication of a number or variable.
• They allow us to simplify expressions and solve equations efficiently.
• Important properties include:
  • Multiplication: a ^m– a ⁿ= a ^m+n
  • Division: a ^m/ a ⁿ= a ^m-n
  • Power of a Power: (a ^m) ⁿ= a ^m*n

Polynomials

Polynomials are expressions consisting of constants, variables, and their exponents. They are classified by their degree, which is the highest exponent of the variable.

• Linear Polynomials: Degree 1, e.g., 2x + 5
• Quadratic Polynomials: Degree 2, e.g., x ²– 3x + 2
• Cubic Polynomials: Degree 3, e.g., 2x ³– 5x ²+ 7x – 1

Operations on Polynomials

Polynomials can be added, subtracted, multiplied, and divided like regular algebraic expressions. However, multiplication requires the use of the distributive property and the FOIL method for binomials.

Factoring Polynomials

Factoring polynomials involves expressing them as a product of simpler factors. This process helps simplify expressions, solve equations, and graph polynomials.

• Common Factoring: Factoring out the greatest common factor.
• Difference of Squares: Factoring expressions of the form a ²– b ²as (a + b)(a – b).
• Sum and Difference of Cubes: Factoring expressions of the form a ³± b ³as (a ± b)(a ²∓ ab + b ²).
• Quadratic Trinomials: Factoring expressions of the form ax ²+ bx + c using the quadratic formula or factoring by grouping.

Unit 5: Rational Expressions and Equations

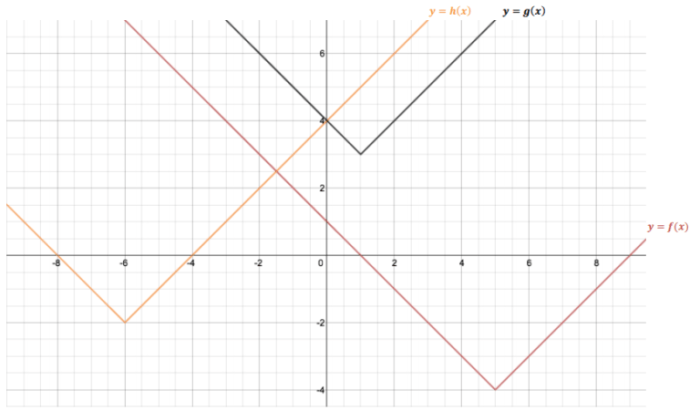
In this unit, we will explore the world of rational expressions and equations, which are mathematical expressions involving fractions of polynomials. We will learn about their properties, simplification techniques, and the different types of rational equations and their solutions.

Defining Rational Expressions

A rational expression is a fraction where both the numerator and the denominator are polynomials. We can simplify rational expressions by factoring the numerator and denominator and canceling out any common factors. This process helps us to write the expression in its simplest form.

Simplifying Rational Expressions

To simplify a rational expression, we can use various methods, such as factoring, canceling common factors, and using the properties of rational expressions. These techniques allow us to rewrite the expression in a more manageable and understandable form.

Solving Rational Equations

Rational equations are equations that involve rational expressions. To solve these equations, we can multiply both sides of the equation by the least common multiple (LCM) of the denominators of the rational expressions. This eliminates the fractions and allows us to solve the resulting polynomial equation.

Unit 6: Radical Expressions and Equations

Radical expressions are mathematical expressions that contain square roots or other roots of variables or numbers. They are used to represent quantities that are not exact squares or cubes, such as the length of a diagonal of a square or the volume of a sphere.Radical

expressions have several important properties. First, the square root of a number is always positive. Second, the product of two radical expressions is equal to the square root of the product of the numbers inside the radicals. Third, the quotient of two radical expressions is equal to the square root of the quotient of the numbers inside the radicals.There

are three main types of radical expressions: square roots, cube roots, and nth roots. Square roots are the most common type of radical expression. They are used to represent the length of a side of a square or the area of a circle.

Cube roots are used to represent the volume of a cube. Nth roots are used to represent the length of a side of an n-dimensional cube.Radical equations are equations that contain radical expressions. They can be solved using a variety of methods, including isolating the radical expression on one side of the equation and then squaring both sides of the equation.

Unit 7: Quadratic Equations and Functions

Quadratic equations are equations of the form ax²+ bx+ c= 0, where a, b, and care real numbers and ais not equal to 0. Quadratic functions are functions of the form f( x) = ax²+ bx+ c.

Types of Quadratic Functions

There are three types of quadratic functions:

• Parabolas that open up ( a> 0)
• Parabolas that open down ( a< 0)
• Lines ( a= 0)

Solving Quadratic Equations

There are three methods for solving quadratic equations:

• Factoring
• Completing the square
• Using the quadratic formula

Solving Quadratic Inequalities

Quadratic inequalities are inequalities of the form ax²+ bx+ c> 0, ax²+ bx+ c < 0, ax²+ bx+ c≥ 0, or ax²+ bx+ c≤ 0.

To solve a quadratic inequality, we can use the following steps:

1. Solve the corresponding quadratic equation.
2. Determine the sign of the quadratic expression for different values of x.
3. Write the solution set as an interval or union of intervals.

Unit 8: Statistics and Probability

Statistics and probability are fundamental branches of mathematics that help us understand and analyze data. Statistics deals with collecting, organizing, and interpreting data to draw meaningful conclusions, while probability focuses on the likelihood of events occurring.

Types of Statistical Measures

Statistical measures provide numerical summaries of data. Common types include:

• Mean: Average value of a dataset.
• Median: Middle value when data is arranged in order.
• Mode: Value that occurs most frequently.
• Range: Difference between the highest and lowest values.
• Standard deviation: Measure of how spread out data is.

Calculating Probability

Probability is a measure of the likelihood of an event happening. It is expressed as a number between 0 (impossible) and 1 (certain). Common methods for calculating probability include:

• Empirical probability: Based on observed data or experiments.
• Theoretical probability: Calculated using known probabilities.
• Conditional probability: Probability of an event occurring given that another event has already occurred.

User Queries: Eureka Math Algebra 1 Module 3

What is the purpose of Eureka Math Algebra 1 Module 3?

Eureka Math Algebra 1 Module 3 aims to provide students with a comprehensive understanding of fundamental algebraic concepts, including linear equations and inequalities, functions, systems of equations and inequalities, exponents and polynomials, rational expressions and equations, radical expressions and equations, quadratic equations and functions, and basic statistics and probability.

What are the key concepts covered in Eureka Math Algebra 1 Module 3?

Eureka Math Algebra 1 Module 3 covers a wide range of key concepts, including solving linear equations and inequalities, graphing functions, solving systems of equations and inequalities, simplifying rational expressions, solving radical equations, understanding quadratic equations and functions, and exploring basic statistics and probability.

How can I access Eureka Math Algebra 1 Module 3?

Eureka Math Algebra 1 Module 3 is typically available through schools or educational institutions that have adopted the Eureka Math curriculum. It may also be accessible online through the Eureka Math website or other educational platforms.